An interval notation calculator is functioned to write numbers in interval notation. Furthermore, it can be written with rectangular brackets or parentheses, and two numbers that will be enclosed with a comma. These two numbers are known as the endpoints of the interval. The left number denotes the least element or lower bound.
However, if you are using a set builder notation calculator you can have interval notation and set builder notation for any numerical statement simultaneously. Roster notation of a set is a simple mathematical representation of the set in mathematical form. In the roster form, the elements of a set are listed in a row inside the curly brackets. Every two elements are separated by a comma symbol in a roster notation if the set contains more than one element. The roster form is also called the enumeration notation as the enumeration is done one after one.
For example, a set consisting of all even positive integers less than 11 is represented in roster form as and in set-builder form, it is represented as . In algebra mathematics, Roster method is used to define sets inside the brackets '()'. The items contained within a set are called elements, and the elements in a set do not repeat in any case. Capital letters are used for denoting sets, whereas small letters are used for denoting elements of the set in curly brackets ''.
This representation of a set notation can be of any elements such as numbers, letters, and so on. For example, the number 5 is an integer, and so it is appropriate to write \(5 \in \mathbb\). It is not appropriate, however, to write \(5 \subseteq \mathbb\) since 5 is not a set.
It is important to distinguish between 5 and . The difference is that 5 is an integer and is a set consisting of one element. Consequently, it is appropriate to write \(\ \subseteq \mathbb\), but it is not appropriate to write \(\ \in \mathbb\). The distinction between these two symbols is important when we discuss what is called the power set of a given set. In Preview Activity \(\PageIndex\), we worked with verbal and symbolic definitions of set operations. However, it is also helpful to have a visual representation of sets.
Venn diagrams are used to represent sets by circles drawn inside a rectangle. The points inside the rectangle represent the universal set \(U\), and the elements of a set are represented by the points inside the circle that represents the set. For example, Figure \(\PageIndex\) is a Venn diagram showing two sets. An online interval notation calculator helps you to find the interval values from the given set interval notation. Also, this set builder notation calculator allows you to find the set builder notation for the given notation.
Apart from set builder & set interval notation, this calculator helps to find total length and topology of the data solution set. So simply add some numbers and leave the rest on this set builder notation calculator to have the final outcomes without doing any manual calculations. When an infinite set is to be represented in a roster set notation, we write a few elements of the set to indicate the defining property of the set followed by three dots.
The set consisting of the objects in one set, say R, but not the other, S, is called the difference of sets and is denoted as R - S. The set consisting of all the elements in sets R and S is called the union of sets and is denoted as R ∪ S. Venn diagrams are visual representations of mathematical sets—or collections of objects—that are studied using a branch of logic called set theory. Set theory is one of the foundational systems for mathematics, and it helped to develop our modern understanding of infinity and real numbers. Therefore, the existence of the Cartesian product of any two sets in ZFC follows from the axioms of pairing, union, power set, and specification.
Roster notation is one of the most simple techniques to represent the elements of a set. A method of listing the elements of a set in a row with comma separation within curly brackets is called the roster notation. Set operations compare the elements in two sets to find commonalities or differences. In MATLAB®, the sets are arrays of numbers, dates, times, or text data.
Most set operations compare sets for exact equality, which can be problematic in the context of floating-point arithmetic. For that reason, the ismembertol and uniquetolfunctions are also available to perform comparisons with a tolerance. Set theory is the mathematical theory of collections of objects. Natural questions that arise in set theory are set membership, overlap, disjointedness and equality. Use Wolfram|Alpha's symbolic capabilities to test for set membership, set equality and subset relations and to draw Venn diagrams.
When trying to perform operations on sets, we can use a tool called Venn diagrams. These diagrams give us a visual representation of sets and allow us to more easily calculate unions, intersections, and differences. To illustrate a Venn diagram, let's use an example.
The contents of a set can be described by listing the elements of the set, separated by commas, inside a set of curly brackets. This way of describing a set is called roster form. A Venn diagram is a visual diagram that shows the relationship of sets with one another. The set of all elements being considered is called the universal set and is represented by a rectangle.
Subsets of the universal set are represented by ovals within the rectangle. Let \(A\) and \(B\) be subsets of a universal set \(U\). For each of the following, draw a Venn diagram for two sets and shade the region that represent the specified set. In addition, describe the set using set builder notation. In mathematics, Set calculator deals with a finite assemblage of objects, be it numbers, letters, or any real-world objects. Sometimes a necessity takes place wherein we require setting up a relationship between two sets.
There comes the concept of set operations and the need of a set finder. In this, a rule, or the formula or the statement is written within the pair of brackets so that the set is well defined. In the set builder form, all the elements of the set, must possess a single property to become the member of that set.
The use of a non-programmable calculator is permitted in this exam. Each object in the set is called an element of the set. If an element x is a member of the set S, we write . If an element x is not a member of the set S, we write . The empty set is the set that contains no elements. For sets A and B, A is called a subset of B, denoted , if every element of A is also an element of B.
Set is a well-defined collection of objects or elements. A Set is represented using the Capital Letters and the elements are enclosed within curly braces . Refer to the entire article to know about Representation of Set in three different ways such as Statement Form, Set Builder Form, Roster Form.
For a Complete idea on this refer to theSet Theoryand clear all your queries. Check out Solved Examples for all three forms explained step by step. Use set builder notation or the roster method to specify the set of integers that are the sum of eight consecutive integers. Use set builder notation or the roster method to specify the set of integers that are the sum of four consecutive integers. In Preview Activity \(\PageIndex\), we learned how to use Venn diagrams as a visual representation for sets, set operations, and set relationships.
In that preview activity, we restricted ourselves to using two sets. We can, of course, include more than two sets in a Venn diagram. Figure \(\PageIndex\) shows a general Venn diagram for three sets (including a shaded region that corresponds to \(A \cap C\)).
Recognize that the union and intersection operations are special because not all set operations satisfy these properties. If we have two sets, A and B, then A - B consists of all of the elements in A but not in B, and B - A consists of all the elements in B but not in A. In this type the endpoints will be included in the interval. Interval set notation calculator is functioned to write in both types. You can pick one just according to the requirement.
Add set builder notation calculator to your website to get the ease of using this calculator directly. Feel hassle-free to account this widget as it is 100% free, simple to use, and you can add it on multiple online platforms. In interval notation method, the starting and the ending number will be represented using the brackets. It has two types of brackets, square bracket and round brackets.
If the interval is mentioned in a square bracket, the end values are included. If the interval is mentioned in round brackets, the end values are not included. So far we specified the elements of sets by verbally.
The roster form introduced here offers a concise way of writing down sets by listing all elements of the set. Furthermore we use ellipsis to describe the elements in a set, when we believe that the reader understands how a pattern in a list of elements continues. When describing ranges in set-builder notation, we could similarly write something like , or if the output had its own variable, we could use it.
So for our tree height example above, we could write for the range . In set-builder notation, if a domain or range is not limited, we could write , or , read as "the set of t-values such that t is an element of the set of real numbers. Before beginning this section, it would be a good idea to review sets and set notation, including the roster method and set builder notation, in Section 2.3. This lesson will review the set operations of unions, intersections, and differences on sets. We will explore these operations with Venn diagrams and look at some properties these operations satisfy.
A set can be defined as a well-structured class or collection of objects. In the builder method or Rule methods set is labelled by a describing property \(P\) of its elements \(x\). It can be read as 'the set of all \(x\) such that \(P\) holds'. The union of two sets A and B is the set of elements which are in A, in B, or in both A and B. Here is a simple online algebraic calculator that helps to find the union of two sets.
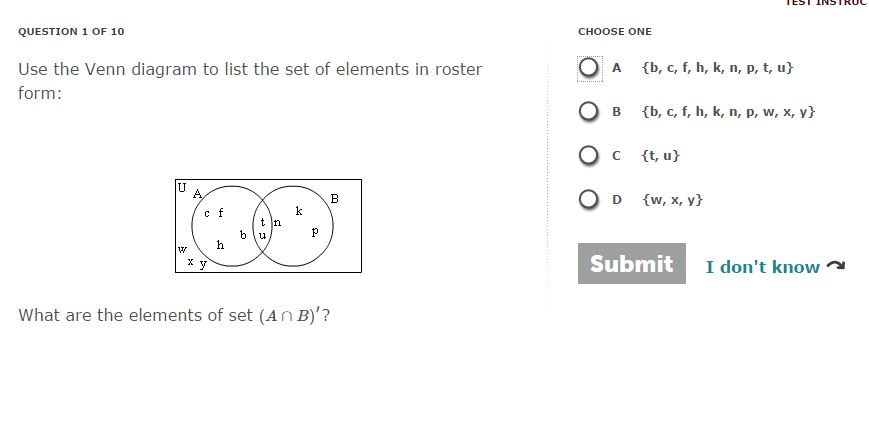
Enter the value of set A and set B as shown and click calculate to obtain the union of two sets. To learn more about the history of Venn diagrams, read our page answering, "What Is a Venn Diagram? " Although John Venn popularized representing set theory with overlapping circles, the ideas and symbols in Venn diagrams actually predate him. The set can be defined by listing all its elements, separated by commas and enclosed within braces. Use Venn diagram to list the set of elements in roster form for A, B, and V. In set roster notation, all elements of a set are listed, the elements being separated by a comma and enclosed within braces .
Set In Roster Form Describe the intervals of values shown on the line graph below using set builder and interval notations. In the previous examples, we used inequalities to describe the domain and range of the functions. This is one way to describe intervals of input and output values, but is not the only way. We need to use set builder notation for the set \(\mathbb\) of all rational numbers, which consists of quotients of integers. We can use Venn diagrams to create a visual representation of a universal set and sets within that universal set. These diagrams can be used to easily calculate operations on sets.
You can also express the set in roster form calculator which will help you find the set and display the result in curly brackets only. The definitions of these numbers may be somewhat elaborate. However, the important thing to realize is that each type of number listed above is aninfinite set, and that set-builder notation is often used to describe such sets.
Let's look at some examples of set-builder notation. This subset calculator can generate all the subsets of a given set, as well as find the total number of subsets. One of the limitations of roster notation is that we cannot represent a large number of data in roster form. For example, if we want to represent the first 100 or 200 natural numbers in a set B then it is hard for us to represent this much data in a single row. This limitation can be overcome by representing data with the help of a dotted line. Take a set of the first 100 positive odd numbers and represent using roster notation.
Given below are 3 Venn diagrams representing three different sets. Let us represent them in roster form step-wise. We will also discover interesting facts about them. Here in the above set representation, the capital letter 'V' represents the set of Odd numbers.
These are separated by commas and enclosed in curly brackets. This calculator is an online tool to find find union, intersection, difference andCartesian product of two sets. It will also generate a step by step explanation for each operation.